薄透镜的傍轴成像
以两个折射曲面为边界的透明体称为透镜,通常多以光学玻璃为材料。
透镜按折射曲面的几何形状可以分为下列几种:球面透镜、轴对称的非球面透镜、柱面透镜以及阶梯透镜(菲涅耳透镜)等。本节只讨论球面透镜,若其中央部分比边缘部分厚,称为凸透镜,反之,则称为凹透镜,如图1。

图1 球面透镜的分类
No.1
物像距公式
设透镜材料的折射率为nL,两侧介质折射率为n与n′,两球面的顶点分别为O1与O2,透镜厚度d=

(图2所示),两球面曲率半径r1与r2未在图中标出。

图2 透镜傍轴成像
分别写出两折射球面的物像距公式:

由图2可以看出,-S2=S′1-d。当d « S′1 以至可以被忽略时,透镜称为薄透镜,此时可认为两球面顶点O1和O2重合并记作O,称为薄透镜光心。现以薄透镜光心O为基准点(在图2中未标出),物距S=OP=S1,像距S′=PO′=S′2,此外S2≈-S′1.将它们代入上面两式,消去S2和S′1,可得

上式称为薄透镜成像的物像距公式。
No.2
焦距公式
依次令物像距公式中S=∞,S'=f '和S'=∞,S=f,即得薄连镜的焦距公式
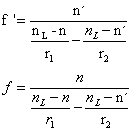
上式表明,薄透镜的两个焦距除了取决于他的几何形状(r1,r2)与材料(nL)外,还与其两侧介质折射率(n,n′)有关,两焦距之比为

可见f和f'符号相同,因此相应的两个焦点F′、F必定分居薄透镜光心O的两侧,一般说来f'与f不等
通常情况下在空气中使用,此时有n=n'≈1,故
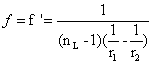
上式称为透镜制造者公式。
若为非薄透镜时,焦距的计算就必须考虑透镜厚度d,故透镜焦距的公式需调整为
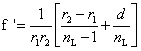
变形为

具有实焦点(f'和f > 0)的透镜叫做正透镜或会聚透镜;具有虚焦点(f'和f < 0)的透镜叫做负透镜或发散透镜。当透镜材料折射率nL大于其两侧介质折射率n,n'时,凸透镜是正透镜,凹透镜是负透镜。
综上所知,凸透镜焦距与凸透镜两个面的曲率半径有关。曲率半径越大,焦距越大,放大倍数越小;曲率半径越小,焦距越小,放大倍数越大。另外,凸透镜焦距还与材料的折射率以及凸透镜所处的环境折射率有关。
已知双凸凸透镜折射率和曲率半径,怎么求焦距?
例子:一曲率半径为50 cm,折射率为1.5的薄平凸透镜使一物体形成大小为物两倍的实像,则该物体的位置应在透镜前___cm。(凸面半径 r值为正,凹面半径 r值为负)
已知:物方的凸面半径r1=50cm,像方的凸面半径r2=-50cm(薄透镜),透镜材料对的折射率nL=1.5,v/u=2,v=2u,求u=?
根据:
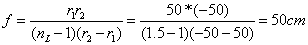
再根据

得:

解得: