
分形几何是现代数学的一个重要概念。一片雪花、一条海岸线,都蕴含着分形的数学规律。认识和运用这样的规律,可以为参数化设计提供宝贵的理论方法。
01 分形几何理论
最早提出分形概念的是美籍数学家曼德布罗特(B . B.Mandelbort)。1967年,他在《科学》杂志上发表了题为《英国的海岸线有多长?》的论文,论证海岸线是一个不确定的量,因为不同的测量维度将得到不同的结果。他指出海岸线是一种极不规则、极不光滑的复杂曲线, 所有的海岸线都存在着这样的不规则性和复杂性, 并且大尺度的海岸线与小尺度的海岸线看上去会十分相似,他称这种相似为“自相似”;他还发现,除海岸线之外,自然中普遍存在着这样的自相似结构,如植物、山川、云水等。曼德布罗特把这些整体与局部以某种方式相似的形体称为“分形”(fractal )。分形一词源于拉丁文,意为“碎片”、“部分”、“不规则”。1975年曼德布罗特出版了《分形: 形状、机遇和维数》一书,创立了分形几何学(fractalgeometry); 1980年, 他用计算机绘制出“自相似集”空间模型,并命名为“曼德布罗特集”(Mandelbort), 同时宣称:整个宇宙以这种自相似结构组成。分形理论出现后迅速被世人关注,并广泛地被应用于数学、哲学、经济学、计算机科学、工程技术学以及艺术设计等众多的领域。
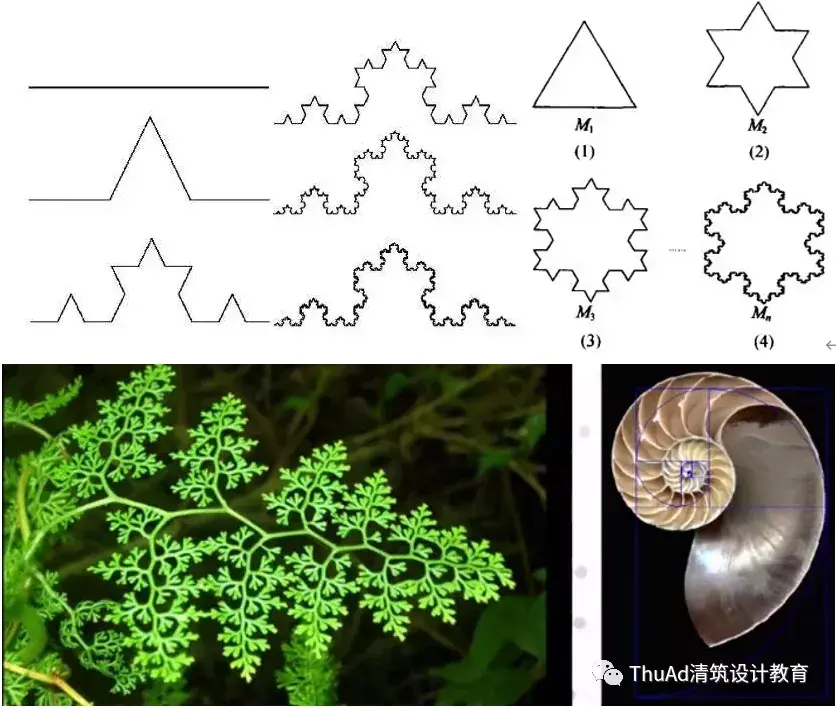

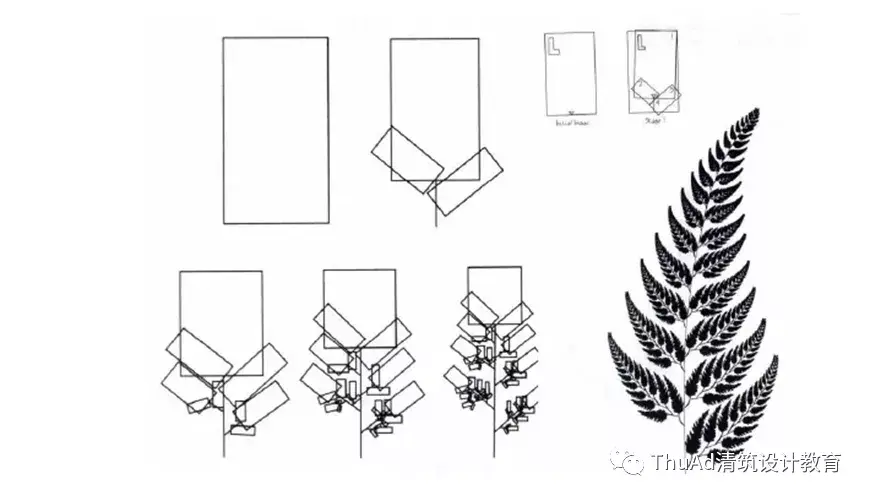
02 设计应用
最早将分形几何理论运用到建筑的是美国德州工农大学的Daniel Koehler,利用单体迭代以及生成规则的制定与复查设计出了一个相对复杂的建筑。

MIT学生宿舍也同样结合布尔运用了分形几何理论的概念进行设计。
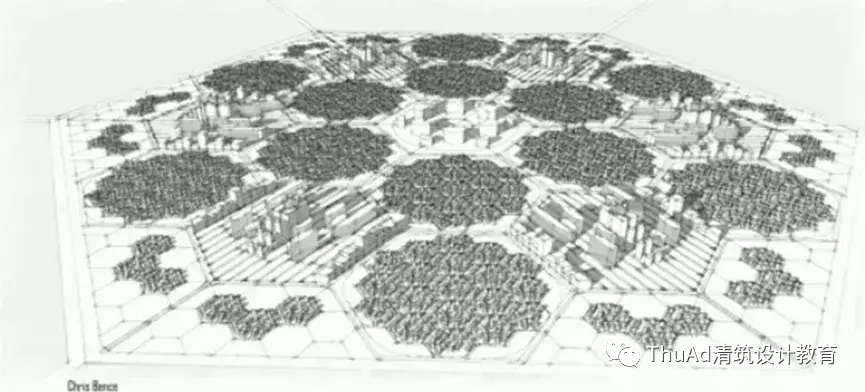
悉尼歌剧院的 “加法建筑学”(additivearchitecture) 理论也仍然着重于自然韵律感和数学美感的完美结合。其多片壳体是从一个完整球面中分割出来的,建筑总体从整体造型,空间布局,到细部构造,表面机理等等的构思来源都得益于球面分割和弧线自我相似形所带来的整体感,创造了分形几何在现代建筑中成功运用的一个完美典范。

“水立方”的建筑表面也是一个典型的分形结构。其设计创意来源于大自然中的水泡和蜂巢,是由不同的六边形结构组成的分形系统,具有强烈的自相似性。但是每一个蜂巢或水泡除了相似性之外,还存在着丰富的非相似性。

湖南长沙松雅湖“伞之丘”同样基于分形几何理论,设想了一种新的建筑原型——以建造过程中的最小结构单元作为基本的空间单元,这些具备某种“自相似性”的基本单元在场地、功能和流线的干预下,不断地生长和集聚,从而构建生成建筑形体——这种建筑从单元演化为整体的过程,就如同生物在自然规律的作用下自然生长一般。

可以说,分形几何理论是一种回归自然、拥抱自然,与自然真正同构的一种设计方法。
 豫恒玖保险柜服务24小时热线-各区售后统一服务实时反馈-今-日-资-讯(豫恒玖保险柜保险柜怎么拧)
2025-09-12 14:17:08
豫恒玖保险柜服务24小时热线-各区售后统一服务实时反馈-今-日-资-讯(豫恒玖保险柜保险柜怎么拧)
2025-09-12 14:17:08
 茉舟保险柜24小时全国售后热线实时反馈-今-日-更-新(茉舟保险柜电子保险柜怎么解锁)
2025-09-12 14:16:43
茉舟保险柜24小时全国售后热线实时反馈-今-日-更-新(茉舟保险柜电子保险柜怎么解锁)
2025-09-12 14:16:43
 茉舟保险柜24小时全国售后热线实时反馈-今-日-更-新(茉舟保险柜电子保险柜怎么解锁)
2025-09-12 14:16:43
茉舟保险柜24小时全国售后热线实时反馈-今-日-更-新(茉舟保险柜电子保险柜怎么解锁)
2025-09-12 14:16:43
 京京保险柜服务热线号码各区24小时维修实时反馈-今-日-资-讯(京京保险柜怎么自制保险柜)
2025-09-12 14:16:22
京京保险柜服务热线号码各区24小时维修实时反馈-今-日-资-讯(京京保险柜怎么自制保险柜)
2025-09-12 14:16:22
 金兽保险柜号码-全国统一400客服24小时服务热线实时反馈-今-日-汇-总(金兽保险柜怎么修改保险柜密码)
2025-09-12 14:14:53
金兽保险柜号码-全国统一400客服24小时服务热线实时反馈-今-日-汇-总(金兽保险柜怎么修改保险柜密码)
2025-09-12 14:14:53