切线方程式是什么（过点的切线方程）

已知一个点在曲线上，求以此点为切点的切线方程？很多人都会做，求出曲线的导函数，在这一点的导数值即为切线的斜率，然后利用点斜式求出切线方程。

当这一点不在曲线上时或此点不是切点时，过此点的直线与曲线相切时，此时直线方程是多少？

虽然不能像最先前的那么做，但也有方法，下面我们来讲解。

题目：

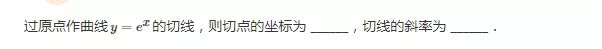
我还加一问，直线方程是多少？

分析：我们要找到切点坐标，因为在切点的导数等于切线的斜率。

设切点坐标为(x0,y0),曲线的导数为：

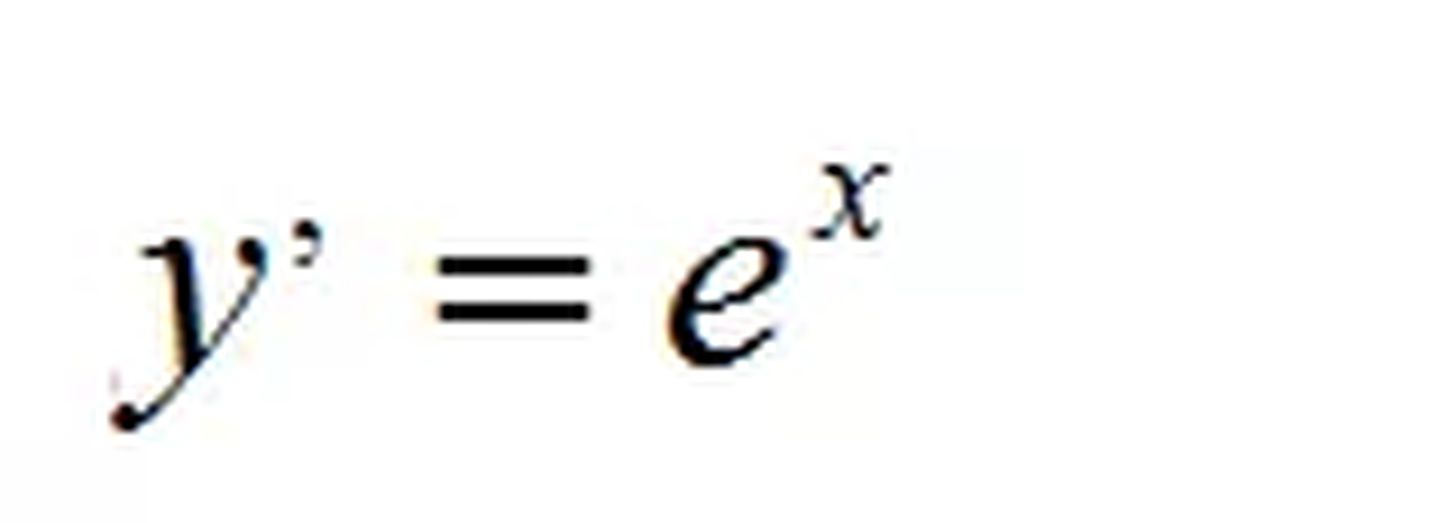
因为在切点的导数等于切线斜率，所以：

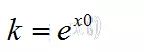
但此时仍没有求出切点或斜率，仍然有未知数，我们来画草图，数形结合：

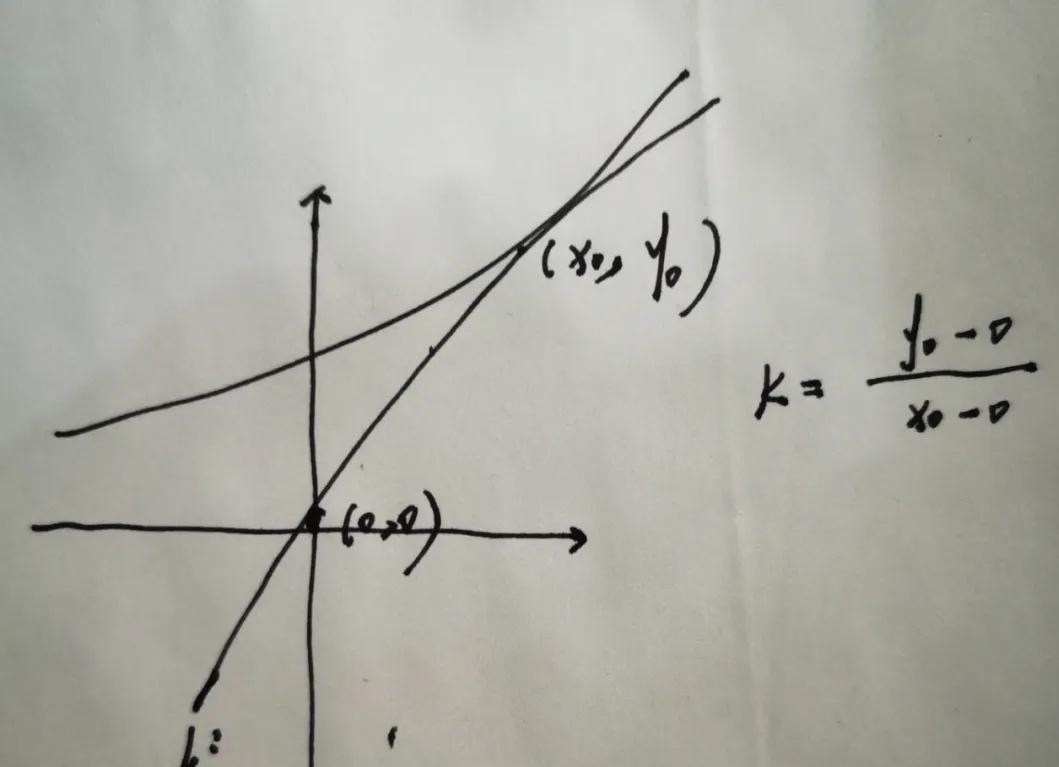
我们发现直线过了切点和已知点，则通过这两点坐标即可求出直线斜率：

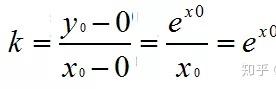
所以求出x0=1，即yo=e,则切线斜率k=e；

所以切线方程：y-e=e(x-1),化简得：y=ex

求过点切线方程总结：(1)设切点坐标，表示出在此点的导数等于斜率；

(2)利用切点和已知点，两点表示出直线斜率；

(3)利用导数表示出的斜率与两点表示出的斜率相等建立关系，求出切点坐标；

(4)求出斜率，利用点斜式写出方程。