角加速度与角速度关系公式（步进电机选型原则）

1、确认步距角

根据定位精度，选择步距角及驱动器细分。

2、电机转矩大于负载转矩：

旋转运动中：

T=Jα

式中：

T一一转矩（相当于直线运动（F=ma）的力），N*m;

J一一转动惯量（相当于直线运动的力）,kg*m^2；

α一一角加速度,rad/s^2;

电机转矩=角加速度x惯量x安全系数

计算时需注意单位统一。单位N*m，kg*m^2，rad/s^2 ，安全系数大于等于2倍。

单位换算举例：

J=20kg*cm^2=0.002kg*m^2

α=10r/s^2=10x2xπ（rad/s^2）

两个方便实用的单位换算公式：

1kg*m*s^2=9.8kg*m^2;

1kg*m=9.8N*m

注：上述两式仅用于计算过程当中，以方便我们的实际工作，由于单位发生了变化，物理意义也就不同了，所以不能简单地将换算后的单位作为原物理量的单位。

角加速度跟转速和加速时的启动时间有关。

角加速度等于角速度的变化率除以变化时间

例如已知：精度为90°±0.5°（0.5°根据实际使用确定，用于选择步进电机的步距角或者细分数。

角加速度=2πn/t

3、保证惯量匹配，电机转子惯量>负载惯量/（5i^2）

注：5为惯量匹配系数，咨询电机供应商，i为减速比，直联时取i=1。

注：转子惯量能满足要求时大部分情况所选电机都能满足要求。

折算到电机轴的转动惯量计算：

（1）带有减速机时

电机惯量Jm；

减速机的惯量为Jg；

减速比为N；

负载总惯量为J负;

加减速机后：

负载总惯量J折算到电机的惯量:J负/(N^2)

总惯量Jtotal：负载总惯量反映到电机的惯量加上减速箱惯量Jg

负载惯量到电机惯量的比率为Jtotal/Jm

（2）直联时：减速比N=1

补充知识：

质心：

质点系的运动不仅与作用在质点系上的力及各质点的质量大小有关，而且与质量的分布情况有关。

质点系的质量中心，简称质心，又称惯性中心。

注：在重力场内，质点系的质心与重心相重合。但应注意，质心与重心是两个不同的概念，质心完全决定于质点系各质点的质量的大小及其分布情况，不论质点系在宇宙空间什么位置它都存在，而重心只是当质点系位于重力场中时才存在。

重心：研究对象的重力的中心，即重心。

物体的重心位置与物体如何放置无关。

对于平面图形，其重心坐标公式如下（注：分割法求解时，切去部分的体积或面积应取负值。）：

式中：

Si一一分割图形的面积（挖去部分的面积取负值）;

xi一一分割图形的形心x坐标；

yi一一分割图形的形心y坐标；

S一一平面图形总面积;

对于均质物体，其重心的位置与其重量无关，而仅与其几何形状有关。物体的几何形状的中心又称为物体的形心。

对于均质物体，其重心和形心位置是重合的。

在工程实际中，构件的形状往往比较复杂。但他们大多数都由一些简单形状的面积或体积组成（如矩形、三角形、圆、球体、主体等）。对于这类问题，可以用分割法把它分成若干简单形体，组成的图形体的重心是容易求得的，然后根据重心坐标公式求出整个形体的重心。

例：

下图为激振器中的偏心轮均质等厚，各部分尺寸为R=10cm，r2=1.3cm，r1=3cm，试确定偏心轮的重心位置。

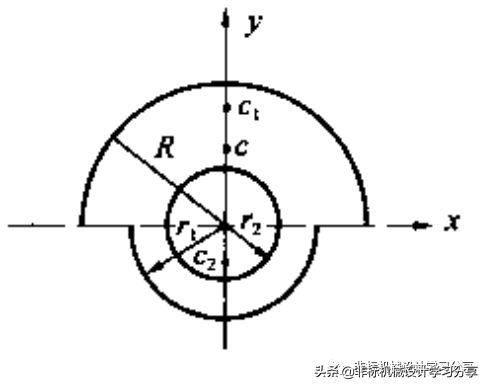
解：

取坐标原点与圆心重合，图形对称于y轴，故xc=0，因此只需求yc，计算过程如下（各部分简单图形的形心位置查常见图形几何形心坐标表）：

转动惯量：

转动惯量是表征刚体转动惯性大小的物理量。

（1）刚体对轴的转动惯量

设有一个刚体及任一轴z（如上图所示），刚体上任一点的质量为mi，与轴z的距离为ri，则各点质量mi与ri2的乘积之和称为刚体对Z轴的转动惯量，用符号Jz表示

注：刚体对某一轴的转动惯量不仅与刚体的质量大小有关，而且与质量的分布有关。

刚体质点离轴越远，其转动惯量越大；反之则越小。

注：对于质量连续分布的刚体，可将上式的质量mi改写为dm，而求和变为求积分，于是有刚体的转动惯量公式：

转动惯量的单位一般为：kg*m2

在工程问题上，计算刚体的转动惯量时，常用下式（当知道转动惯量时，可用该式求解刚体回转半径）：

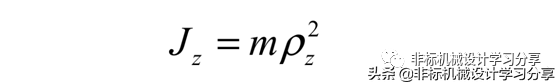
式中：m为整个刚体的质量，ρz为刚体对z轴的回转半径。

值得注意的是，回转半径只是在计算刚体的转动惯量时，假想地把刚体的全部质量集中在离轴距离为回转半径的某一圆柱面上，这样在计算刚体对该轴的转动惯量时，就简化为计算这个圆柱面对该轴的转动惯量。

几种转动惯量计算公式：

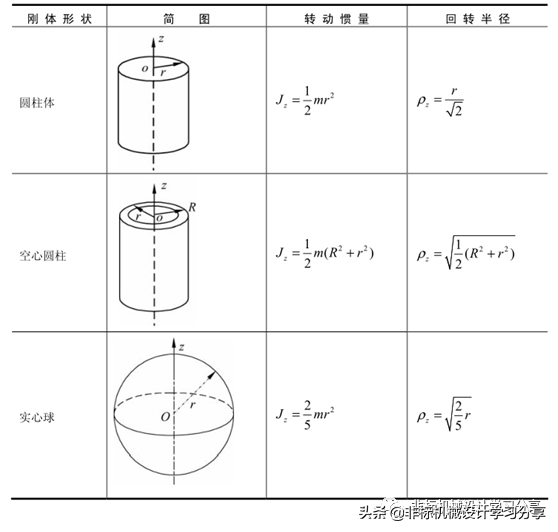
平行轴定理（刚体对通过质心的轴和与它平行的转动惯量之间的关系。）：

刚体对于任意轴的转动惯量，等于其通过质心、并与该轴平行的轴的转动惯量加上刚体的质量与两轴间距离平方的乘积，即

注：同一刚体对不同轴的转动惯量一般是不同的。在所有平行轴中，刚体对通过质心的轴的转动惯量最小。

例：

（1）铸铁偏心轮的半径R=10cm，厚度b=5cm，偏心距e=2cm，如下图所示。铸铁的密度ρ=7300kg/m^3,求此偏心轮对偏心轴的x’的转动惯量。

解：

此偏心轮的重量P=πR^2bρ=πx0.1^2x0.05x7300=11.5N

其质量为M=P/g=11.5/9.8=1.17kg

此偏心轮对通过重心（质心）的轴x的转动惯量，可按均质圆柱体计算，如下：

Jx=（1/2）MR^2=1/2x1.17x0.1^2=0.00585kg*m^2

偏心轮对偏心轴x’的转动惯量可应用平行移轴定理，即：

J’x=Jx+Me^2=0.00585+1.17x0.02^2=0.00632kg*m^2

（2）均质圆盘与均质杆组成的钟摆如下图。已知圆盘质量m1，直径为d，杆的质量为m2，长l，试求钟摆对悬挂轴o的转动惯量Jo。

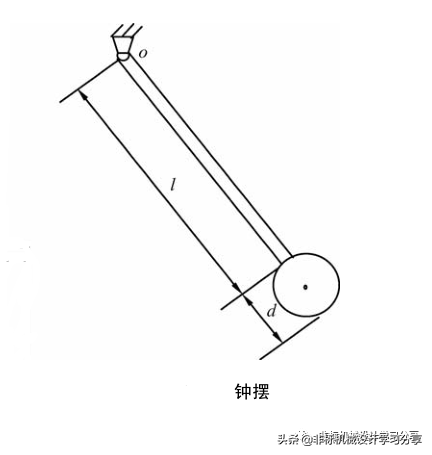
解：

钟摆由均质杆和均质盘组成，所以有：

Jo=Jo杆+Jo盘

其中

所以：