
圆锥曲线的光学性质源于它的切线和法线的性质,因而为正确理解与掌握其光学性质,就要掌握其切线、法线方程的求法及性质。
设P(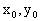 )为圆锥曲线
)为圆锥曲线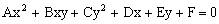 (A、B、C不同时为零)上一定点,则在该点处的切线方程为:
(A、B、C不同时为零)上一定点,则在该点处的切线方程为: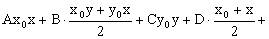
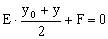 。(该方程与已知曲线方程本身相比,得到的规律就是通常所说的“替换法则”,可直接用此法则写出切线方程)。
。(该方程与已知曲线方程本身相比,得到的规律就是通常所说的“替换法则”,可直接用此法则写出切线方程)。
该方程的推导,原则上用“△法”求出在点P处的切线斜率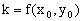 ,进而用点斜式写出切线方程
,进而用点斜式写出切线方程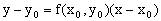 ,则在点P处的法线方程为
,则在点P处的法线方程为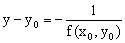
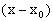 。
。
1、抛物线的切线、法线性质
经过抛物线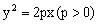 上一点作一条直线平行于抛物线的轴,那么经过这一点的法线平分这条直线和这一点的焦半径的夹角。如图1中
上一点作一条直线平行于抛物线的轴,那么经过这一点的法线平分这条直线和这一点的焦半径的夹角。如图1中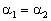 。
。

事实上,设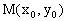 为抛物线
为抛物线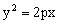 上一点,则切线MT的方程可由替换法则,得
上一点,则切线MT的方程可由替换法则,得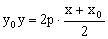 ,即
,即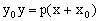 ,斜率为
,斜率为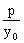 ,于是得在点M处的法线方程为
,于是得在点M处的法线方程为
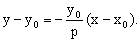
令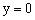 ,得法线与x轴的交点N的坐标为
,得法线与x轴的交点N的坐标为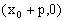 ,
,
所以
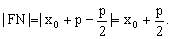
又焦半径
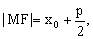
所以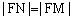 ,从而得
,从而得 即
即
当点M与顶点O重合时,法线为x轴,结论仍成立。
所以过M的法线平分这条直线和这一点的焦半径的夹角。
也可以利用点M处的切线方程求出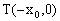 ,则
,则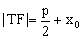 ,又故
,又故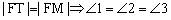 ,从而得
,从而得
也可以利用到角公式来证明
抛物线的这个性质的光学意义是:“从焦点发出的光线,经过抛物线上的一点反射后,反射光线平行于抛物线的轴”。
2、椭圆的切线、法线性质
经过椭圆上一点的法线,平分这一点的两条焦点半径的夹角。如图2中
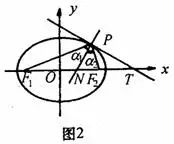
证明也不难,分别求出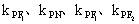 ,然后用到角公式即可获证。
,然后用到角公式即可获证。
椭圆的这个性质的光学意义是:“从椭圆的一个焦点发出的光线,经过椭圆反射后,反射光线交于椭圆的另一个焦点上”。
3、双曲线的切线、法线性质
经过双曲线上一点的切线,平分这一点的两条焦点半径的夹角,如图3中。仍可利用到角公式获证。
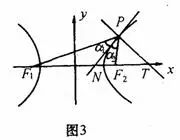
这个性质的光学意义是:“从双曲线的一个焦点发出的光线,经过双曲线反射后,反射光线是散开的,它们就好像是从另一个焦点射出的一样”。
--END-
 暮暮里保险柜售后24小时联系方式维修查询实时反馈-今-日-更-新(暮暮里保险柜电子保险柜怎么换电池)
2025-09-12 11:24:52
暮暮里保险柜售后24小时联系方式维修查询实时反馈-今-日-更-新(暮暮里保险柜电子保险柜怎么换电池)
2025-09-12 11:24:52
 信一保险柜售后24小时联系方式维修查询实时反馈全+境+到+达(信一保险柜保险柜怎么选)
2025-09-12 11:24:20
信一保险柜售后24小时联系方式维修查询实时反馈全+境+到+达(信一保险柜保险柜怎么选)
2025-09-12 11:24:20
 艾莱仕保险柜全国24小时服务热线400统一客服服务热线(艾莱仕保险柜保险柜忘记密码怎么开锁)
2025-09-12 11:23:42
艾莱仕保险柜全国24小时服务热线400统一客服服务热线(艾莱仕保险柜保险柜忘记密码怎么开锁)
2025-09-12 11:23:42
 星航保险柜全国各市售后服务点热线号码实时反馈-今-日-资-讯(星航保险柜家用保险柜怎么选)
2025-09-12 11:22:41
星航保险柜全国各市售后服务点热线号码实时反馈-今-日-资-讯(星航保险柜家用保险柜怎么选)
2025-09-12 11:22:41
 艾谱保险柜售后维修号码-人工售后号码实时反馈全+境+到+达(艾谱保险柜怎么隐藏保险柜)
2025-09-12 11:18:11
艾谱保险柜售后维修号码-人工售后号码实时反馈全+境+到+达(艾谱保险柜怎么隐藏保险柜)
2025-09-12 11:18:11